My research is in the interdisciplinary area of computational physics, effective field theories, lattice gauge theory, and mathematical physics.

During my Ph.D. studies in physics at Washington University in St. Louis, I had the unusual opportunity to work simultaneously on two completely independent subjects. Having two thesis advisors, Prof. Claude Bernard and Prof. Carl Bender, I was able to work on diverse topics from lattice gauge theory to mathematical physics. During my postdoctoral research, I continued working on those topics. Moreover, I introduced a project to determine quark masses with a novel method, and I employed different skills that I learned from my advisors in the project, which resulted to three related papers (a trilogy) and led to very precise determination of the masses of five of the six quarks found in Nature.

On this page, you see a list of my scientific projects during my doctoral and postdoctoral research. I only mention the papers that I was one of the main coauthors with a significant amount of contribution, and I mainly describe my contribution to the papers.

• Quark Masses
• Decay Constants and Search for New Physics
• Nonlinear Eigenvalue Problems
• Strange Quark Condensate
• Form Factors and Search for New Phyics
• Decay Rate of eta mesons

Quark Masses

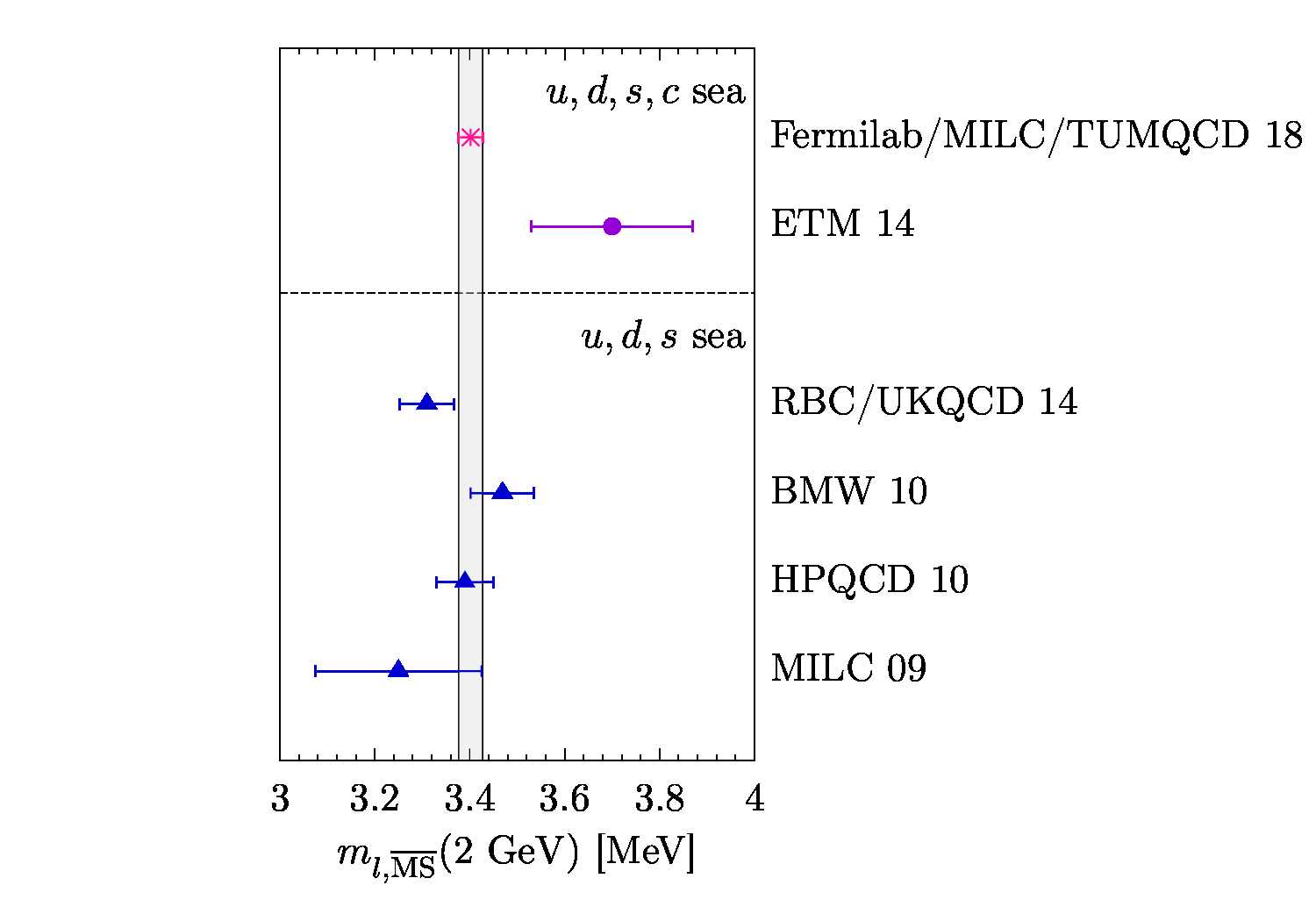
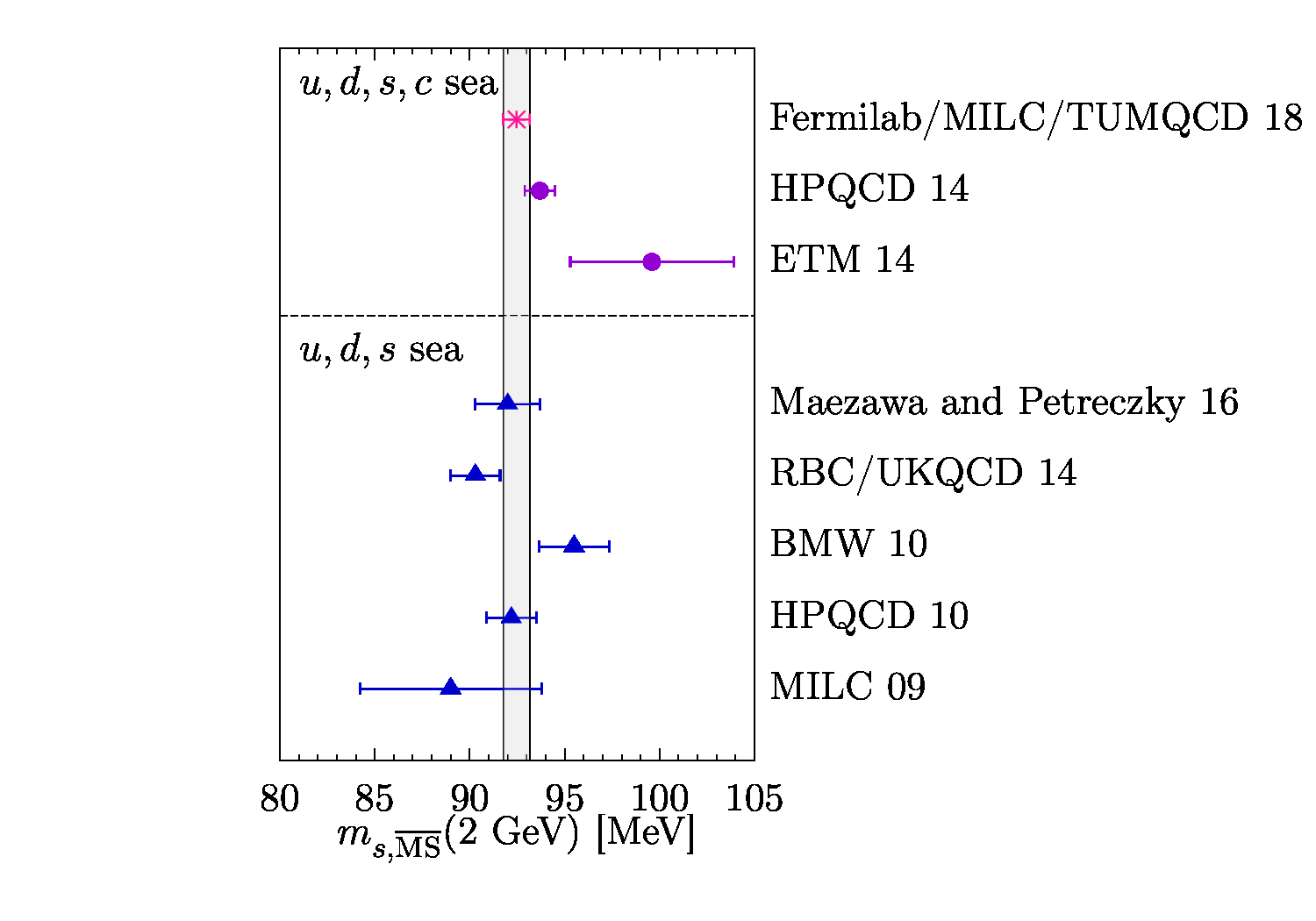
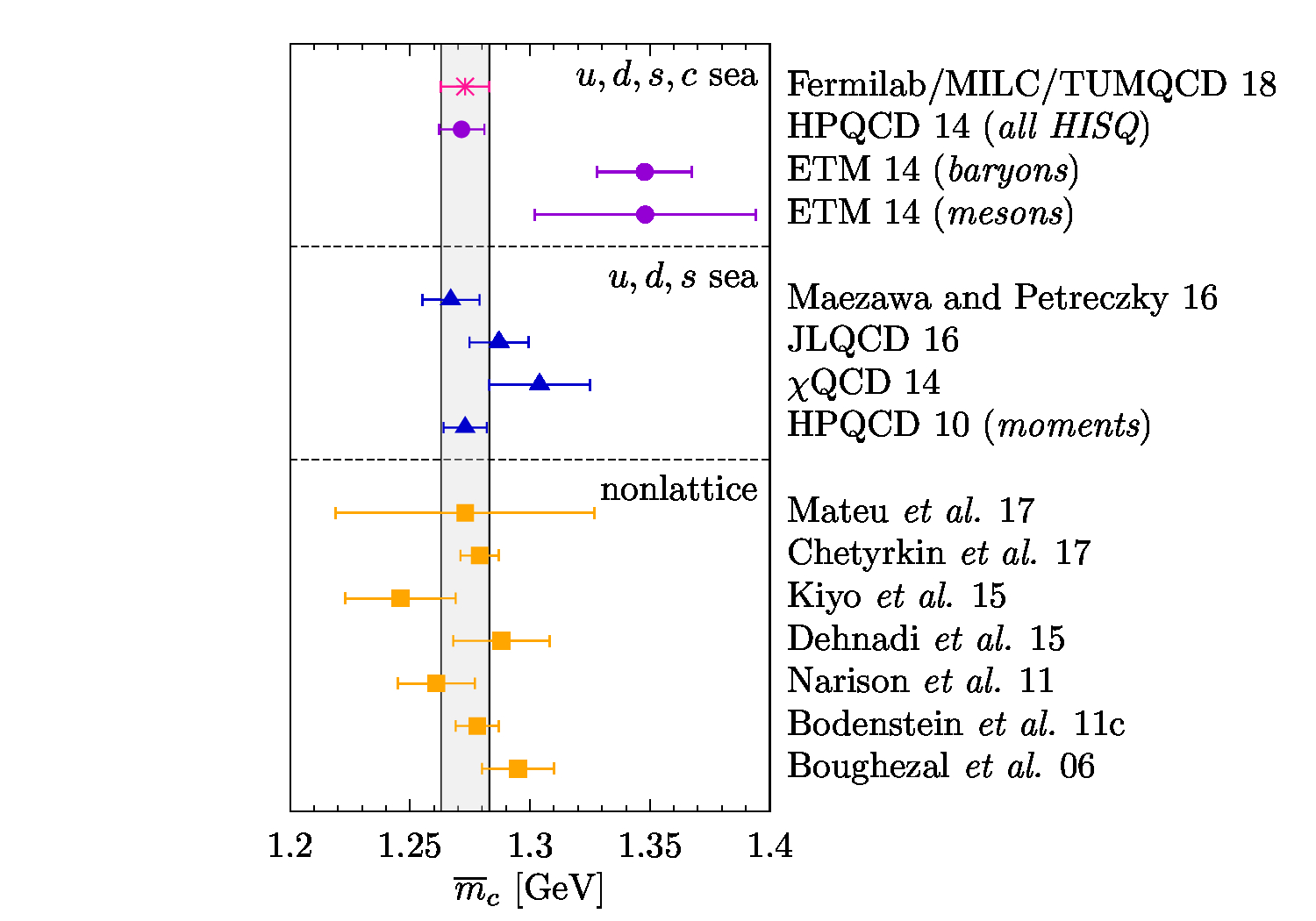
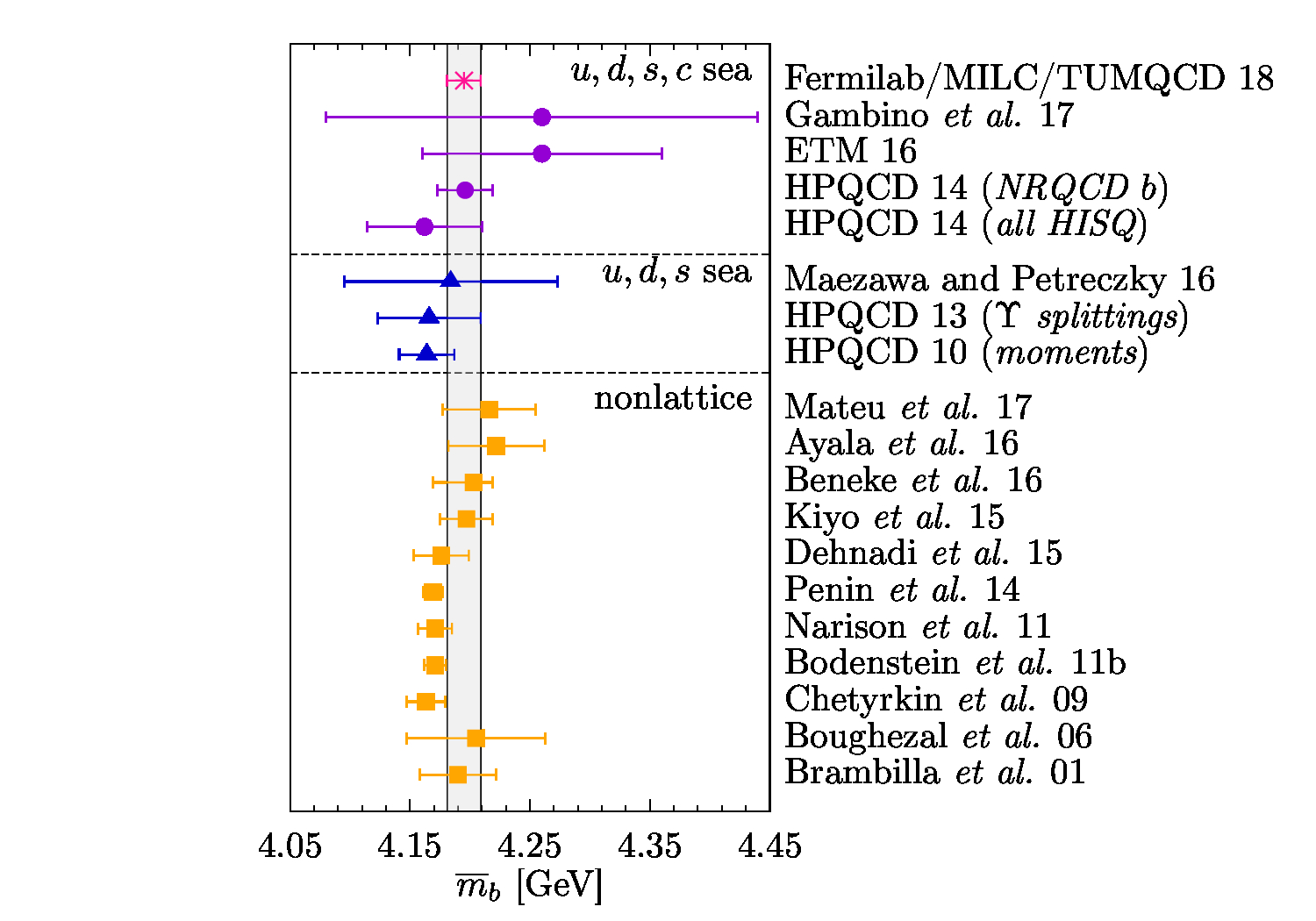
A trilogy of papers describe my work on the determination of quark masses:

1. A discussion on leading renormalon in the pole mass,
2. Relations between Heavy-light Meson and Quark Masses,
3. Up-, down-, strange-, charm-, and bottom-quark masses from four-flavor lattice QCD.

I describe this project as the one that I am most proud of. In ten seconds you understand why! This project was indeed a complex work in the interdisciplinary area of computational physics, effective field theories, lattice gauge theory, mathematical physics, and statistical analysis. I am proud because of two reasons. First, I proposed the idea from scratch; it was my own child. Second, although the idea looked very straightforward, its successful implementation required a diverse set of skills that, fortunately, I either had or learned. The work led to a very precise determination of the masses of five of the six quarks found in Nature and their ratios.

Let me start with a comment that is not obvious for non-theoretical physicists. The conventional notion of the rest mass of an object, such as the Sun, the Earth, your smartphone, a piece of paper, or even an electron, cannot be straightforwardly used for particles like quarks that are confined in hadrons such as a proton. Because it requires a good deal of theoretical work, it is the job of theoretical physicists---not experimentalists---to measure (calculate) the masses of quarks. Theoretical physicists have developed their conventions, also called schemes, of defining and measuring the masses. The most common one is the so-called MS-bar scheme; people usually report their results in this particular scheme. Let me now present a chronological report of my idea of calculating quark masses.

I started thinking about the idea when I was in St. Louis in the last year of my Ph.D. studies and proposed the idea in the Fall of 2015 when I went to Munich, as a postdoctoral researcher. The idea looked nice and simple, and my colleagues liked me working on it and determine the masses of quarks. As the devil always comes from details, I encountered many problems when I tried to implement the idea.

The idea was novel and simple looking: generate data with lattice-QCD simulations, build a function based on effective field theories to model the data, fit the function to the data, and finally, use the parameters of the fit function as well as a set of experimental inputs to determine the masses of quarks. From the numerical point of view, the most expensive part was the first part that required generating a large amount of lattice-QCD data. Fortunately, I did not even need to worry about this part because the MILC collaboration was generating the required data for a different project: determination of decay constants of heavy-light mesons.

This project included several layers of analyses, starting from the analysis of lattice-QCD correlators, which was done by Doug. This was followed by a layer of analysis that included scale setting and determination of the ratio of light quark masses, namely the ratio of the average of the up and down quark masses to the strange quark mass. In a parallel process mainly led by Claude, the ratio of the up and down quark masses was determined using a lattice setup that included both QCD and QED effects. Those layers of analyses were common with the decay constant project. I was in charge of the next layers up to calculating the final results presented in the paper. Andreas, Antonio, Claude, Doug, Nora, and Ruth were in the subgroup that directed the research. The rest of the coauthors of the last paper of the trilogy were involved in the project mainly at the stage of generating lattice-QCD data. The work was also influenced by Prof. Marteen Beneke because of his valuable comments on the first paper of the trilogy.

From the numerical point of view, the lattice-QCD data that I worked with in 2015 were not as clean as the final data that I used in 2018 when the last paper of the trilogy was published. During those years my colleagues, especially Doug, generated more lattice data, which improved the statistics. As the statistics improved, his analyses evolved and led to cleaner data. Moreover, Doug and Claude investigated the effect of freezing of topological charge on the lattice data, and they incorporated their results in the analysis.

Along with improving the lattice-QCD statistics, the model that I used for fitting the data evolved during the project from a very simple model to a sophisticated one. The model initially was designed to yield only the charm and bottom quark masses without including the light quark masses and their effects in simulations. As an intermediate quark mass, we first employed the kinetic mass and, later on, the renormalon-subtracted mass. Both of these intermediate masses were employed to circumvent the so-called renormalon divergence in the pole mass of quarks. None of them led to satisfying results, so I decided to improve the model by investigating the renormalon divergence in the pole mass.

My efforts to improve the model led to the first and second papers of the trilogy. In the first one, I investigated the pattern of the renormalon divergence in the pole mass and found a recursive relation that governs the large-order behavior of the pole mass in perturbation theory, leading to the renormalon divergence. Based on the recursive relations, I obtained a sum rule to calculate the overall strength of the renormalon divergence and incorporated the result in the model. In the second paper of the trilogy, I investigated two aspects of relating the mass of a heavy-light meson to the masses of its quark-antiquark components. First, I introduced a novel definition for a quark mass, the minimal-renormalon-subtracted (MRS) mass, which was free from the shortcomings of the other intermediate masses used initially in the work. Using a skeleton of effective field theories, which was originally developed by Claude and me for the decay constant project, and employing the MRS mass, I presented a sophisticated, practical formula to relate meson masses to quark masses. After I finished the draft, Andreas' eloquence improved the draft to a very well-written one. Antonio's and Nora's critical reading of the draft and valuable comments polished the draft such that it left the referee nothing to object to. The paper also benefited from Claude's suggestions in its early stages.

Let me now highlight a part of the second paper related to the MRS mass

As explained in Ref. [73], "an asymptotic series ... is a compact encoding of a function, and its divergence should be regarded not as a deficiency but as a source of information about the [underlying] function." The crucial point here is that, equipped with the overall normalization [8], we could decode the divergence due to the leading infrared renormalon in the pole mass. Then we could recover the contribution of this renormalon in the form of the nonperturbative function \(J_\text{MRS}(\bar m)\), which has a convergent expansion in powers of the reciprocal of \(\alpha_s(\bar m)\), rather than in powers of \(\alpha_s(\bar m)\) itself.

I conclude this part by mentioning that our determination of quark masses attracted widespread attention, including an invitation to address the plenary session of the 36th International Symposium on Lattice Field Theory (2018) and the plenary session of XIIIth Conference on Quark Confinement and the Hadron Spectrum (2018). Furthermore, I contributed to a review paper:

4. Strong coupling constant and quark masses from lattice QCD,

Decay Constants and Search for New Physics

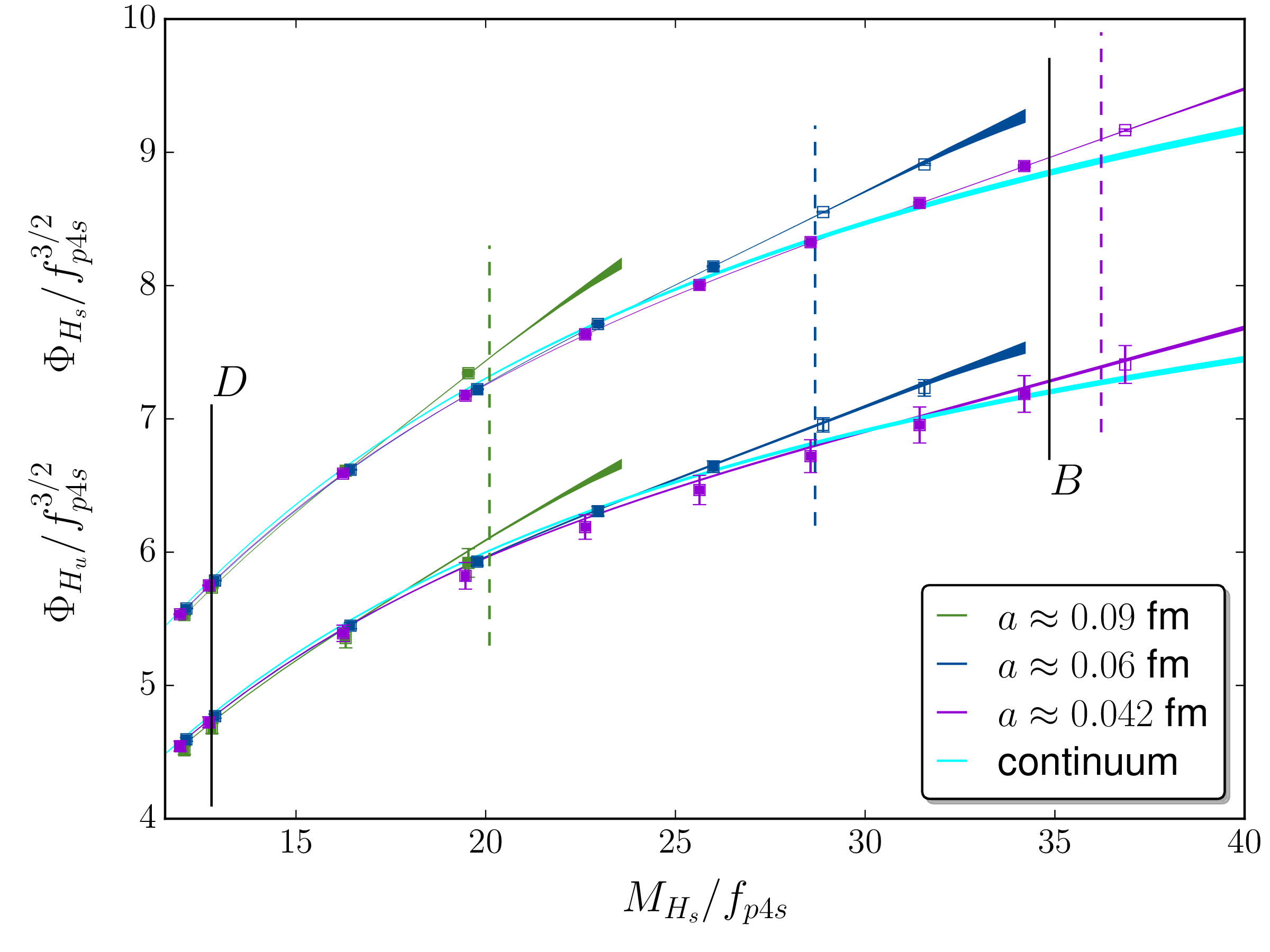
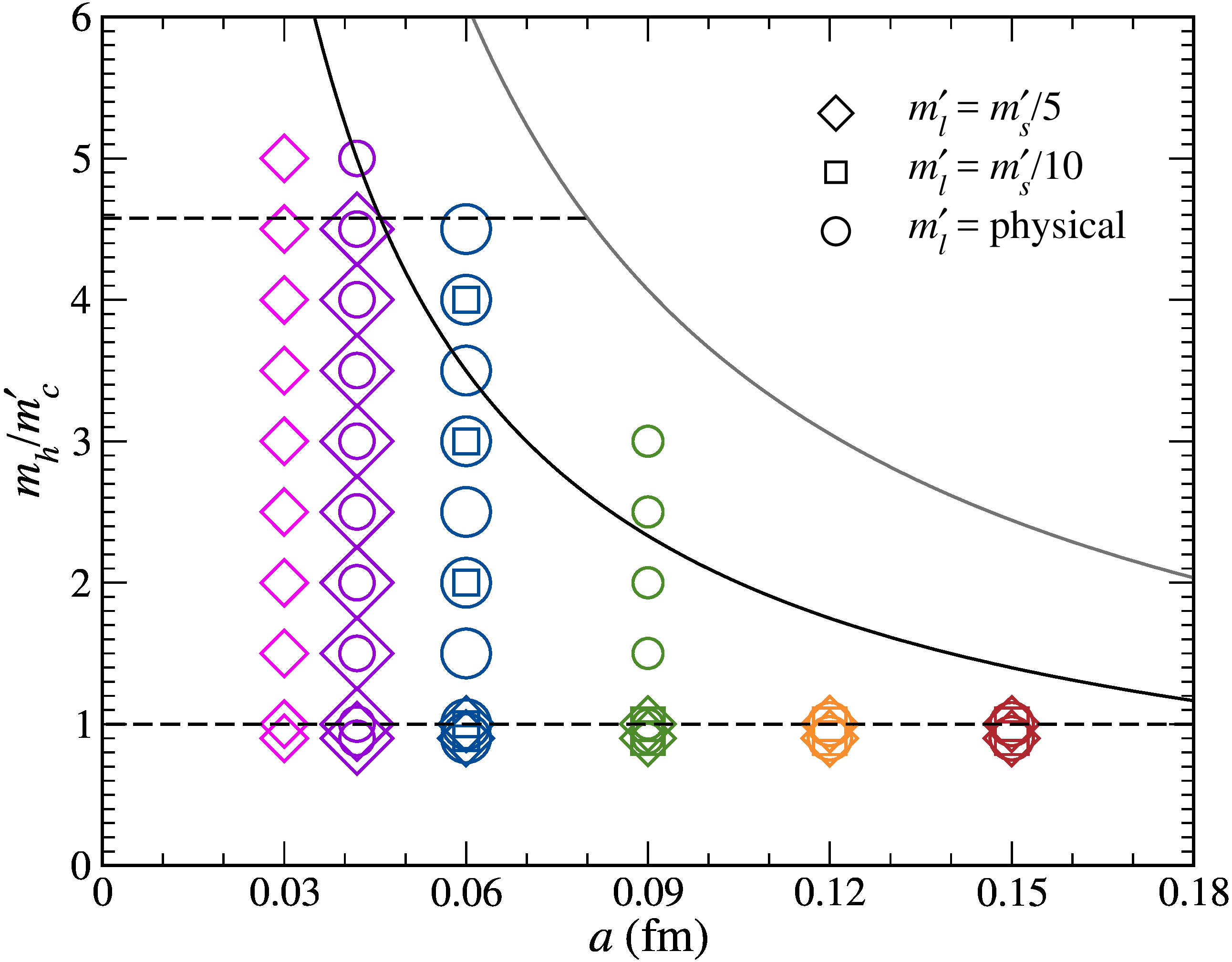
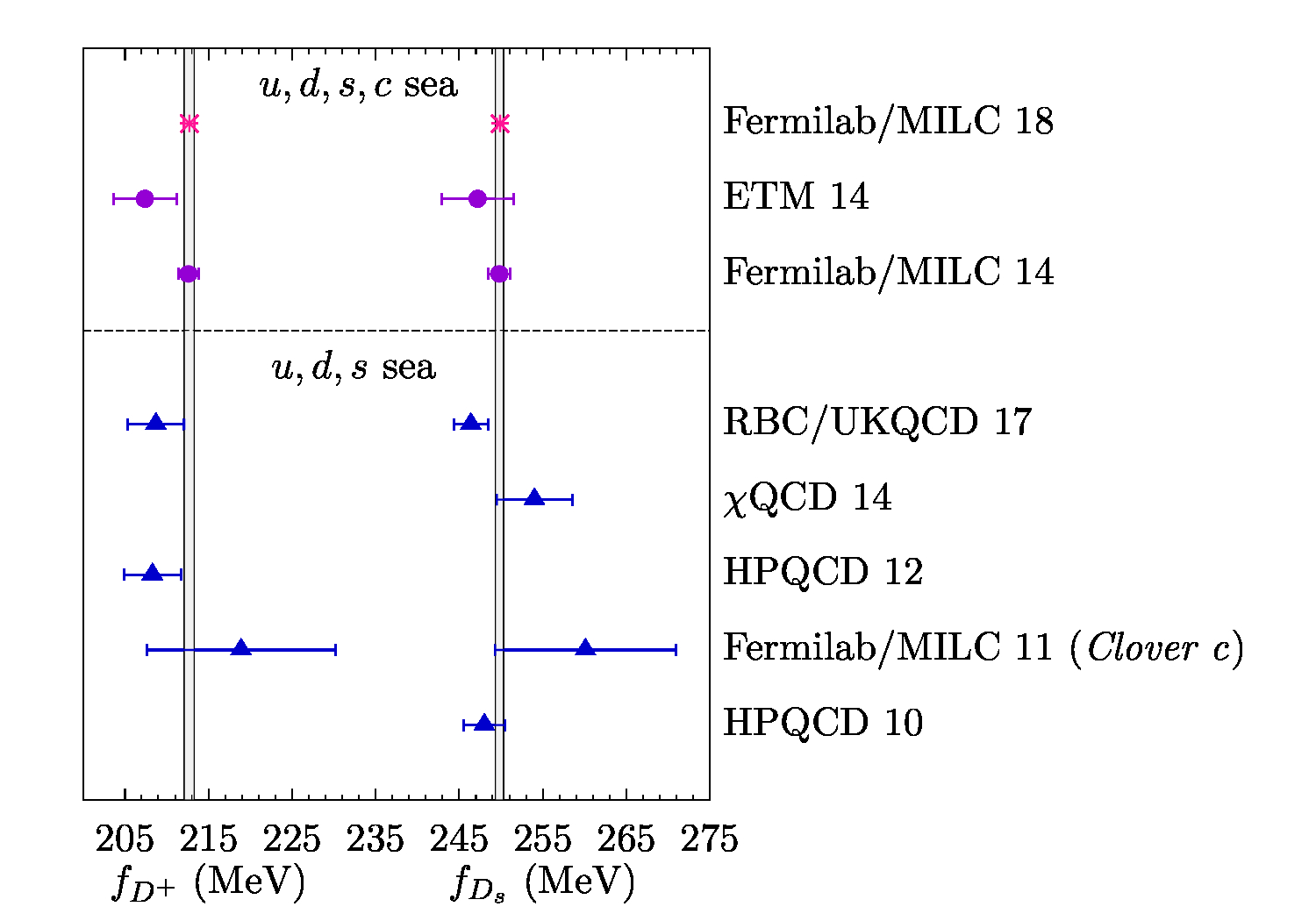
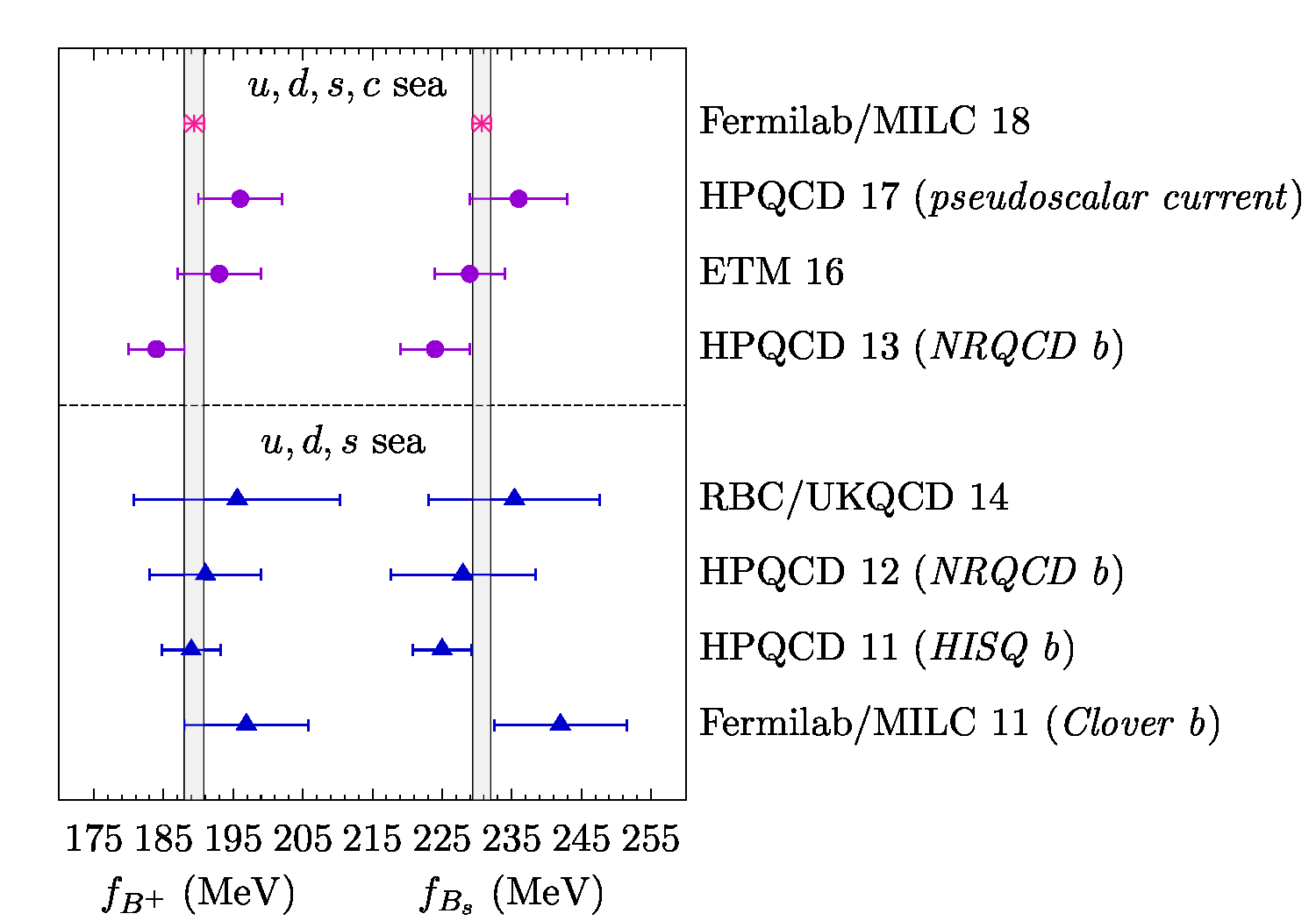
I have been one of the key contributors of a project by the FNAL and MILC collaboration on the determination of decay constants of heavy-light mesons using lattice-QCD simulations. In short, these decay constants are useful in the search for New Physics beyond the Standard Model, and that's why it was an important project.

A trilogy of papers describe my work related to this project:

1. Chiral Perturbation Theory for All-Staggered Heavy-Light Mesons,
2. Charmed and light pseudoscalar meson decay constants from four-flavor lattice QCD with physical light quarks,
3. B- and D-meson leptonic decay constants from four-flavor lattice QCD.

Applications of the results of the first paper led to the second paper of the trilogy published in 2014, using a part of the data, and to the third one published in 2018, using the complete set of the data. (The lattice data used in this project were generated by the MILC collaboration during more than six years: before 2012 till the end of 2017.) In the third paper, we presented the most precise determination of the \( D \) and \( B \) meson decay constants and their ratios. Our results for the \( B \) meson decay constants were three times more precise than the previous best lattice-QCD calculations, and brought the QCD errors in the standard model predictions for the rare leptonic decays \(B_s \to \mu^+ \mu^-,\) \(B^0 \to \mu^+ \mu^-,\) and their ratios to well below other sources of uncertainty.

I should emphasize that the work published in the second and third papers included several layers of heavy computations and analyses. The first layer, done by the MILC collaboration, was generating lattice-QCD ensembles and measuring the so-called two-point correlators on the lattices. The second layer was to statistically analyze the correlators, followed by a layer of analysis that included scale setting and determination of the ratio of light quark masses, namely the ratio of the average of the up and down quark masses to the strange quark mass. Doug performed those layers of analyses. In a parallel process mainly led by Claude, the ratio of the up and down quark masses was determined using a lattice setup that included both QCD and QED effects. Andreas, Claude, Doug, Ruth, and I were on the committee of the project, and I was the main force in performing the next layers up to calculating the decay constants in the continuum limit. (Claude was my Ph.D. supervisor when we wrote the second paper of the trilogy, and Andreas was my postdoctoral mentor when we wrote the third one.) By the way, the phenomenological aspects of the project were worked out by Ruth.

A part of the analyses was common between this project and my other project on the determination of quark masses, described above.

Nonlinear Eigenvalue Problems

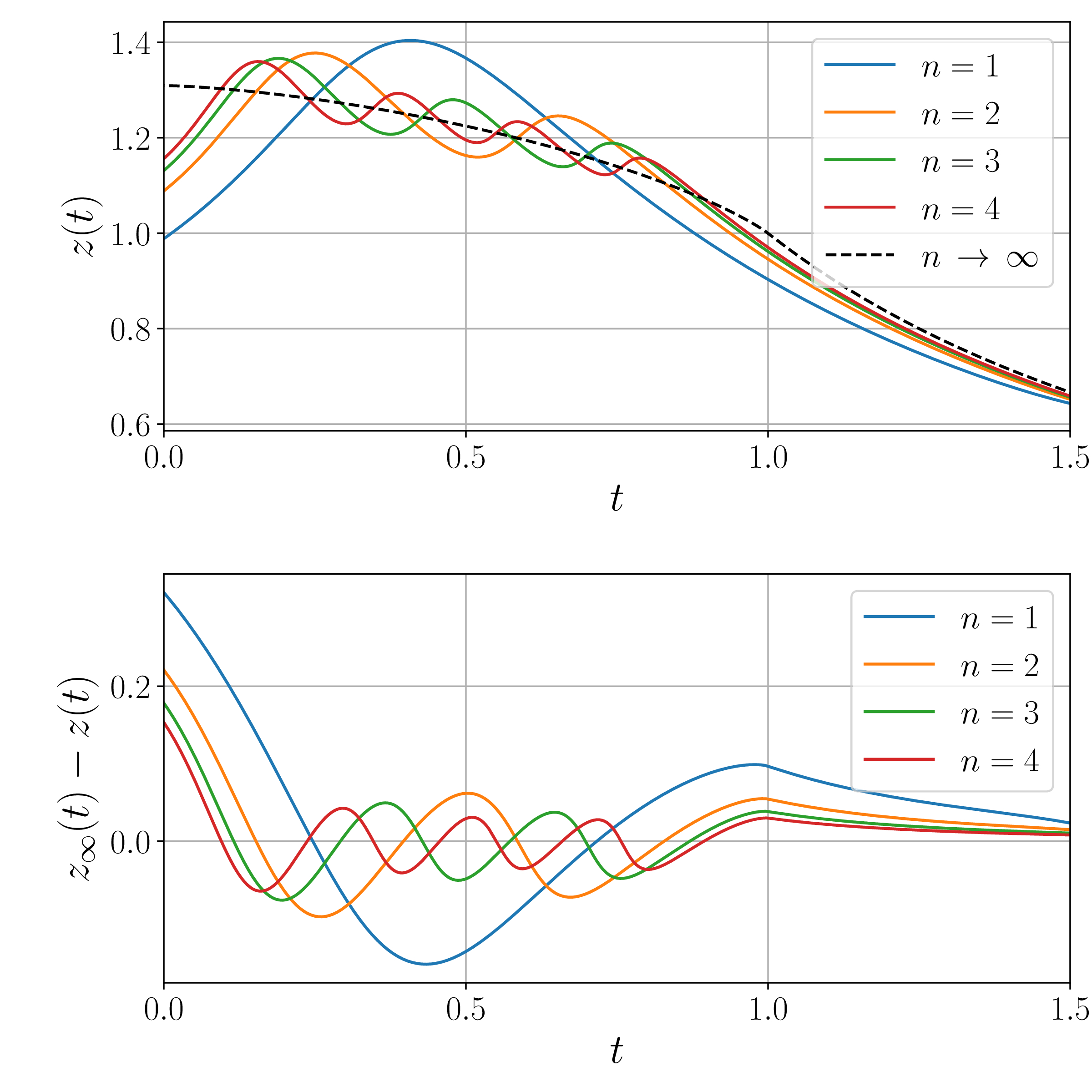
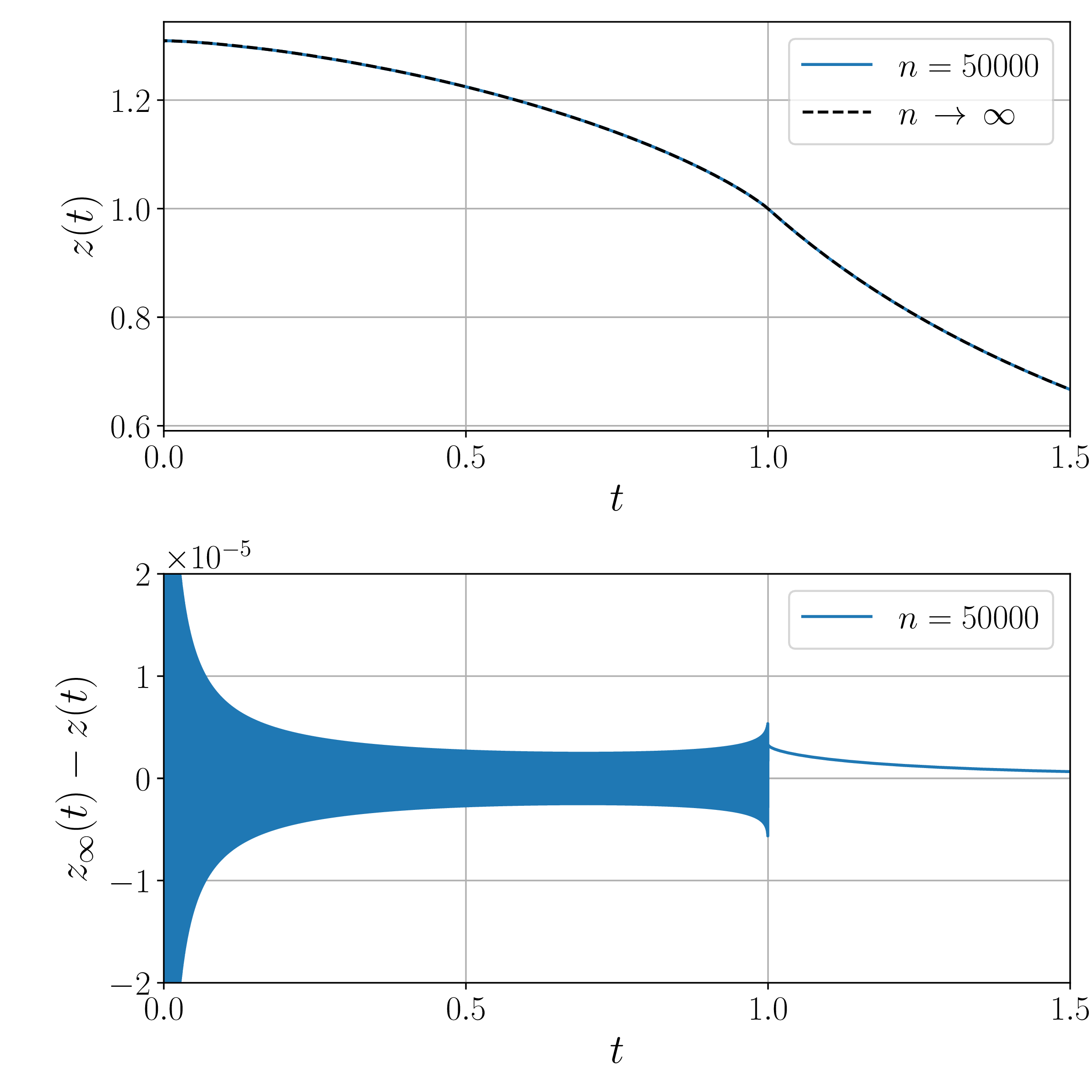
My Ph.D. thesis contained two completely independent parts. The idea of nonlinear eigenvalue problems was the subject of the second part, which was my research under the supervision of Prof. Carl Bender. We published two papers

1. Nonlinear Eigenvalue Problems,
2. Painleve Transcendents and PT-Symmetric Hamiltonians,

We found that, for each equation, there are one or more discrete sets of initial conditions that lead to unstable separatrix behavior. We identified these discrete sets as eigenvalues of the corresponding problems and worked out their asymptotic behaviors by reducing each problem to a linear one.

Let me give a chronological report about this project. The whole project started from one of Carl's lectures on advanced mathematical methods in the Fall semester of 2012; the ''Physics 503'' course. One day he talked about the first Paineleve equation and explained a phenomenon that is shown in Fig. 4.9 of his book. I tried to understand the phenomenon using a simpler equation: the Ricatti equation. Right after his lecture, I asked him if the Ricatti equation shows the same phenomenon, and he told me something along the lines of: why don't you solve the equation numerically to find out what happens?

I tackled both the Ricatti and the first Painleve equations and showed the results to Carl. He immediately realized that the initial values (or slopes) follow an algebraic asymptotic form. By the way, the solutions resembled quantum wave functions, and thus we called the initial values/slopes as the eigenvalues of the problem. Later on, I extended the study to the second Painleve equation and found similar behavior. Carl suggested me to investigate a simpler equation: \( y'(x) = \cos(\pi xy) \), which is a first-order nonlinear differential equation, unlike the Painleve equations that are second order. (This equation was given as an exercise in the text by Bender and Orszag.)

Our numerical investigation indicated that the eigenvalues of \( y'(x) = \cos (xy) \) asymptotically grow as \( A \sqrt{n} \), and we used Richardson extrapolation to calculate the coefficient \( A \) to an accuracy of one part in \( 10^{10} \) and we conjectured reliably that \( A = 2^{5/6} \). At this point, Carl told me to solve the problem analytically because, as he told, the coefficient \( A \) cannot be an algebraic number, unless there is an analytic solution to the problem. I could find an analytic solution by reducing the problem to a one-dimensional random-walk problem.

Carl and I continued our work. Here are three more papers that we have published after my Ph.D. studies:

3. Nonlinear eigenvalue problems for generalized Painleve equations,
4. Fourth Painleve Equation and PT-Symmetric Hamiltonians,
5. First-order nonlinear eigenvalue problems involving functions of a general oscillatory behavior,

Quark Condensate

....

Form Factors and Search for New Physics

....

Decay Rate of eta_c and eta_b

....